https://www.toutiao.com/a6756788128960217604
这是一道面试题:如何在海量数据(如亿级数据)中判断某个数据是否存在?
回想一下,在java中我们可以使用列表、集合等数据结构来存放数据,如hashmap,然后判断某个数据是否存在,但在此问题中显然不适用,因为上亿的数据在内存较小的计算机中无法存放。
通常我们有以下解决思路:
将海量数据分散存储到多个文件中去,依次将每个文件载入内存进行判定;
使用多台机器进行分布式计算,每台机器完成各自任务;
使用布隆过滤器(Bloom Filter)。
本篇主要介绍第三种方法:布隆过滤器 。
我们先熟悉一下 位图 的概念。
位图也叫 位数组 , 可以看成 是一个数组,每个 数组 单元只 存储“0 ”或者“1”,每个 单元 大小为 1bit 。

正是因为位图所需内存较小,所以这里可派上用场。
上文说了,位图存放的是0和1,那么怎么和实际数据对应起来呢?很自然能想到使用 哈希函数 。
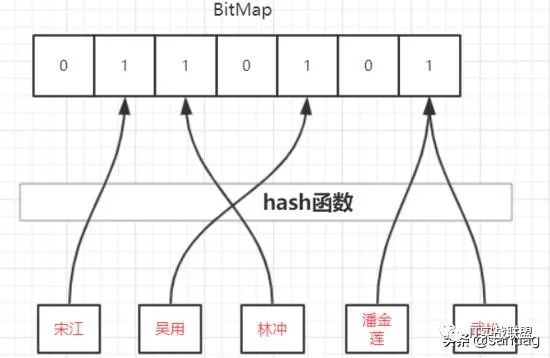
如图,将人名存进位图时,可使用hash函数,将人名映射到对应的位图单元中,并将该单元数值置为1,0则代表没有数据映射到该单元,即该单元没有存放数据。
然而 hash冲突 是不可避免的,图中可看到“潘金莲”和“武松”散列到了同一个数组单元。这就出现了一个问题:假如我们要存储的数据中有“潘金莲”,没有“武松”,当我们对“武松”进行哈希后发现其对应位置为1,于是认为“武松”存在于该数据集中,显然这个结果是错误的,因为1是潘金莲的映射结果。
那么怎么解决这个问题呢?因为hash冲突不可避免,所以我们只能尽量减少冲突的发生。
一般有两种思路:
对位图扩容,使用容量更大的位图;
rehash。
事实上,大名鼎鼎的 布隆过滤器(Bloom Filter) 使用的便是这两种思路。看下百度百科给出的定义。
布隆过滤器(Bloom Filter)是1970年由布隆提出的。它实际上是一个很长的 二进制 向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都比一般的算法要好的多,缺点是有一定的误识别率和删除困难。
简单而言,布隆过滤器就是 位图+一系列随机映射函数 。
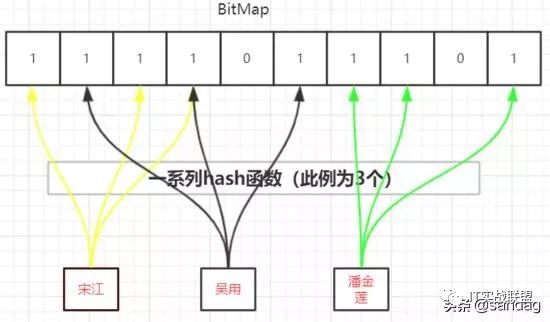
如上图,使用了三个互相独立的hash函数,对每条数据都进行三次哈希,并将对应单元置为1.
这样能减少hash冲突的发生,当然hash函数的个数以及位图的容量是视情况而定的。
布隆过滤器的优点:
1.每个单元只占1bit , 所用空间小;
2.使用哈希直接查找 , 查询时间短 。
布隆过滤器的 缺点:
1.由于hash冲突的存在 ,有一定的 误判率 ;
2.由于hash冲突的存在 , 删除数据较为困难 。
先看误判率。
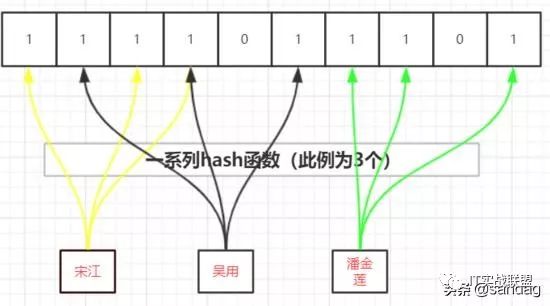
其实与刚才“武松和潘金莲”的问题类似:假设“吴用”并不在数据集中,但它的位置已被其它数据置为1,那么判定结果会错误。
但如果“吴用”对应的某个位置为0,那么“吴用”必定不存在,因为如果存在,与其对应的所有位置都为1.
由此可得下面两条结论:
布隆过滤器判断数据存在,那么它可能存在也可能不存在 。
布隆过滤器判断数据不存在,那么它必定不存在。
再看删除数据。
这个也好理解,举个栗子。
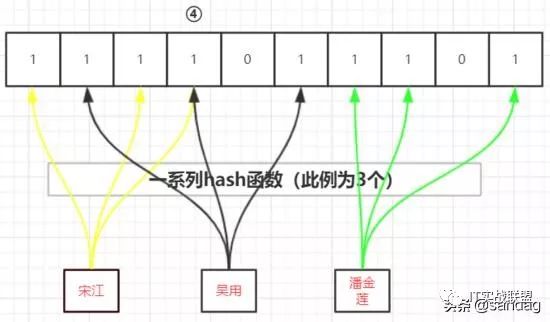
“吴用”和“宋江”都映射到④号位置,现在想要删除“吴用”,那么④号位置到底要不要置为0呢?如果置为0,那么“宋江”就不高兴了,如果不变,显然又会增加对“吴用”的误判率(已经被删除,但该位置还是1)。
在后来的改进中,对位图的每个单元增加了 计数器 ,计数器初始值为0,每映射一个数据,计数器加1,每删除一个数据,计数器减1。这样在删除数据时,只要计数器 当前值 大于1,该单元就不置为0.
布隆过滤器的应用场景有很多,典型的有Redis的缓存穿透、爬虫时URL去重、垃圾邮件的判别等。
注意:本文归作者所有,未经作者允许,不得转载
